Étude : les exemples concrets en math moins efficaces
 La science de la réalité ne se contente plus du comment phénoménologique; elle cherche le pourquoi mathématique. (Gaston Bachelard)
La science de la réalité ne se contente plus du comment phénoménologique; elle cherche le pourquoi mathématique. (Gaston Bachelard)
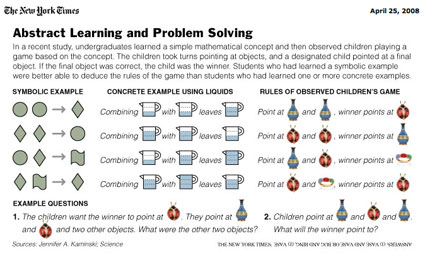
Une étude jette un doute important sur la croyance fort répandue en mathématiques, semble-t-il, selon laquelle la représentation de situations concrètes favorise l’apprentissage (EurekAlert! Concrete examples don’t help students learn math, study finds; New York Times : Study Suggests Math Teachers Scrap Balls and Slices). Selon des chercheurs du Center for Cognitive Science (Université Ohio State), le recours au concret nuit à la transférabilité des savoirs, une qualité mieux servie par l’abstraction.
L’étude a été menée auprès d’étudiants d’âge collégial, de sorte qu’on ignore si le phénomène vaut aussi pour le secondaire ou le primaire. Des pédagogues des mathématiques, tel que Gilles, sauront mieux que moi trancher cette question. Néanmoins, j’ose une hypothèse de réponse.
Les notions se construisent généralement du simple au complexe, de même que des savoirs antérieurs aux savoirs périphériques. Par conséquent, on gagnera à faire évoluer l’élève du concret à l’abstrait, dans la mesure où l’abstraction est à sa portée. De plus, on peut supposer que les exemples concrets conviennent davantage aux mathématiques de base et les symboles aux mathématiques plus avancées.
Gardons cependant à l’esprit que l’élève, dans son être, doit battre son propre sentier, plus ou moins accidenté et semé d’imprévus. En outre, son aptitude à jongler avec des abstractions mathématiques varie en fonction de sa nature. Le devoir du pédagogue consiste donc à ne pas lui imposer, mais à s’éclairer, des formules de la science.
(Image thématique : 24, par Jan Weiss)
Par ricochet :
Origami, art et mathématiques
Certaines habiletés mathématiques seraient innées
Ressources interactives en math en fonction de l’âge
Stimuler la pensée mathématique
Mathcasts : un wiki de screencasts mathématiques
Merveilles d’imagerie mathématique
Illustrer les maths avec Flickr / partager pour apprendre
Mathématiques occidentales vs asiatiques
Partenariat école-université profitable aux math et sciences
Les math comme indicateur de réussite en sciences
Simplifier l’enseignement des mathématiques?
Vous pouvez suivre les commentaires en réponse à ce billet avec le RSS 2.0 Vous pouvez laisser une réponse, ou trackback.








Bonjour,
Il est difficile de prétendre que le concret ne favorise pas l’apprentissage. D’abord, il faut penser que les maths ont été inventées afin de comprendre l’environnement d’abord et d’agir sur lui ensuite. Enlever le concret, c’est couper les maths de leur source et de leur aboutissement.
L’apprentissage à partir du concret pose cependant des problèmes lorsque les situations concrètes constituent des exemples non généralisables. Ainsi, présenter la multiplication telle une addition répétée, que ce soit à l’aide de représentations concrètes ou symboliques,ne peut conduire qu’à un échec au moment d’aborder la multiplication de fractions, la multiplication de relatifs ou la multiplication algébrique. Ce n’est probablement pas l’apprentissage à partir du concret qu’il faut remettre en question, mais l’apprentissage à partir de certains exemples concrets (ou symboliques).
Par ailleurs, associer l’abstrait au symbolique plutôt qu’au concret constitue, à mon avis, une erreur. Ma petite fille, qui n’a que deux ans, fait de nombreuses abstractions, sans pouvoir en parler ou rédiger de document écrit à leur sujet. Il n’y a aucun doute que l’abstraction précède, et de loin, le symbolisme. En fait, abstraire consiste à générer des concepts et cela se fait d’abord à partir du concret. L’observation de très jeunes enfants le démontre aisément.
Enfin, doit-on apprendre du simple au complexe ou, au contraire, apprendre consiste-t-il à simplifier le complexe ?
Essayons d’apprendre au bébé à parler en n’utilisant que les verbes du premier groupe au présent durant sa première année d’existence et en ajoutant par la suite les autres temps, puis les autres groupes. Personne ne fait cela et pourtant, dans l’environnement langagier extrêmement complexe dans lequel il évolue, l’enfant met de l’ordre et finit par parler correctement. Mieux encore, plus cet environnement langagier est évolué, plus l’enfant utilisera très tôt un langage évolué. Et, que penser de ces enfants de 4 ans qui parlent très bien deux, trois ou même quatre langues sans accent alors que ceux qui ont d’abord appris seulement une langue ont par la suite énormément de difficultés à en apprendre une seconde ?
Bref, il me semble que la preuve est faite depuis longtemps à l’effet qu’il faut rejeter certaines représentations concrètes au moment d’aborder l,apprentissage d’un concept, mais cela ne démontre nullement que l’apprentissage à partir du concret, je dirais même, l’apprentissage accompagné continuellement du concret ne peut pas être rejeté si facilement.
Je vous remercie de tant d’éclairage M. Lyons. Il est toujours hasardeux, en effet, de séparer radicalement des concepts interreliés. Les généralités, non plus, n’aident pas. La distinction du concret et de l’abstrait est d’ailleurs fort délicate, considérant que notre représentation du concret est en soi une abstraction, un fait que Magritte a fameusement mis en évidence dans son tableau Ceci n’est pas une pipe.
Il en est de même du rapport entre le simple et le complexe. Un objet n’a de sens que dans son rapport avec la complexité de son environnement. Je crois que l’association gagne à être bilatérale (ou multilatérale).
Je suis de votre avis quant à l’importance en éducation de lier les concepts à la réalité. Celle-ci, cependant, ne peut pas toujours retenir la pensée. À dire vrai, ils dépendent l’un et de l’autre.
Je suis totalement d’accord avec M. Lyons.
J’ajouterais quelques points.
0. En maths, les exemples (et contre-exemples) sont importants pour, je pense, s’assurer qu’une définition est bien comprise.
1. En maths, il faut faire attention aux «images». Je pense à tous ces livres de maths qui illustrent les entiers en les plaçant sur une droite numérique. D’abord, qui dit que les négatifs sont « à gauche » et les positifs « à droite »? Et puis, qui dit que la « distance » entre 1 et 2 doit être la même que la distance entre -3 et -4 ALORS QUE LA SOUSTRACTION N’A PAS ENCORE ÉTÉ DÉFINIE!!!
2. Je fais beaucoup de programmation informatique avec les enfants (SCRATCH, SQUEAK). Récemment, dans une classe, j’ai illustré le potentiel d’un code par un exemple. À peu près tous les enfants sont restés «bloqués» sur l’exemple. Dans un autre groupe où je n’ai fait aucun exemple, les enfants se sont lancé et ont tous produit des idées originales à partir du code…
3. Je reviens sur ta phrase : «Les notions se construisent généralement du simple au complexe [...]» En fait, je suis à peu près convaincu du contraire. Les notions, les concepts sont construits à partir de l’organisation intelligente du chaos. C’est en «organisant» les forêts, l’air, la vie que l’homme en est venu à penser aux atomes, et non l’inverse. Un enseignant, c’est quelqu’un qui aide les élèves à voir une organisation dans le complexe, tout en l’amenant à découvrir et exprimer sa propre vision.
Il est à la fois agréable et rassurant de compter parmi ses lecteurs des esprits tels que Robert Lyons et Gilles Jobin. Et d’autant plus quand on s’aventure hors de son champ d’expertise.
La relation entre le simple et le complexe continue de me chicoter. Puisque que nous baignons, dès la naissance, dans un environnement complexe, l’antériorité revient forcément à ce dernier. La compréhension des phénomènes est donc d’abord affaire d’analyse. C’est dans un deuxième temps que la construction à laquelle je faisais allusion entre en jeu, dans le processus de synthèse qui tend de la simplicité des éléments à la complexité du nouvel objet.
Il ne faut cependant pas considérer ce processus comme linéaire. Il est davantage rétroactif et synergique, de sorte que la question de l’antériorité ne se pose pas en ces termes.
En lisant un compte-rendu de la recherche mentionnée plus haut, je me suis souvenu de deux phénomènes observés à maintes reprises. La première consiste en la capacité importante des élèves, dès le début du primaire à générer des lois correctes à partir d’éléments purement symboliques. Cela est observable, par exemple, au moment où ils tentent de résoudre des équations avec un seul terme manquant. Pour plusieurs élèves ce travail n’est relié à rien de concret. Or, les termes manquants leur sont présentés progressivement et on peut observer qu’à chaque étape, ils génèrent des lois qui englobent tous les cas précédents et le nouveau cas. La nouvelle loi remplace toujours les lois précédentes contredites par le nouvel exemple.
Par ailleurs, lorsqu’on propose un problème en l’associant à une situation concrète, avec ou sans support matériel entre les mains des élèves, ils se cantonnent dans cette représentation concrète et «la jouent à fond». Ainsi, ayant associé des morceaux de gâteau à diverses représentations symboliques, j’ai demandé aux élèves (4e année) d’ordonner les représentations symboliques afin d’indiquer laquelle représentait le moins de gâteau jusqu’à celle qui en représentait le plus. Or, plus de la moitié des élèves prétendaient que 2/4 représentait moins de gâteau que 1/2. Interrogés, ils ont mentionné qu’en coupant un gâteau en 4 parties, on faisait plus de miettes qu’en 2 parties et qu’on ne mangeait pas les miettes.
À plusieurs reprises, les élèves m’ont démontré que les réponses qu’ils écrivent dans un test n’étaient pas suffisantes pour porter un jugement éclairé sur leurs apprentissages réels.
J’oserais ajouter un autre point. Il ne me semble pas surprenant que les élèves à qui on a présenté de nombreuses et diverses concrétisations d’un concept ne puissent facilement en déduire une forme générale. Je ne suis pas certain que de les comparer à des élèves qui ont eu une présentation d’un modèle généralisable, bref à des élèves qui n’ont pas eu à faire l’effort d’abstraction d’une forme généralisable en partant de quelques concrétisations soit valable.
J’ignore si ce qui suit constitue un bon exemple, mais pour fin de discussion, … enfin, nous verrons. Prenez la racine carrée, cette semaine encore un élève de 8 ans me disait que c’était le nombre qui, multiplié par lui-même, donne le nombre dont on extrait la racine. Beaucoup d’adultes connaissent cette définition pourtant, ils sont étonnés d’apprendre que la racine carrée est la longueur du côté d’un carré dont …
La loi des signes est aussi bien connue des adultes, mais peu de gens l’associent à la langue parlée dans laquelle ils ont pourtant compris que deux négations remplacent une affirmation.
J’aimerais revenir sur le passage complexe – simple – complexe mentionné précédemment par François. Pour l’instant, je cherche exemples et contre-exemples. Hum, encore une nuit qui s’annonce agitée.
À bientôt.
Ces exemples sont tous plus fascinants les uns que les autres. Celui des gâteaux est particulièrement savoureux
Je n’aurais pas cru les enfants capables de tant de prouesses d’abstraction. Cela démontre encore une fois notre incapacité à se mettre dans la tête d’un enfant. Je crois que dans sa maturation, le cerveau peu difficilement, sinon est incapable, de concevoir comment il était à un stade antérieur. On réussit bien à garder des souvenirs, mais sait-on réellement percevoir les choses de la même façon que ne le faisait notre cerveau plus jeune? Certains référents, à tout le moins, sont forcément absents.
Je crois que j’ai péché en ne précisant pas mieux ce que j’entends par simple. Si je peux me racheter, un peu tard, je n’entends pas la simplicité comme un élément qui se rapproche de l’unité ou de l’indivisible, mais plutôt comme un élément qui nous est familier, au point de représenter un élément de sens (un schème, comme dirait Kant). La notion de symbole chez un enfant, par exemple, ne peut donc découler que d’un objet familier préalable. Du moins, la première fois que l’esprit en synthétise le sens. Une fois la notion saisie (familière), il peut créer tous les symboles qu’il veut.
Il me semble que la précision de François au sujet de la distinction entre le simple et le complexe peut nous aider. Prenons la conduite d’une automobile, perçue comme fort complexe par le débutant et simple après quelques heures de pratique. En y pensant bien, un problème ou un travail quelconque ne varie pas en complexité avec le temps, c’est notre adaptation à ce travail qui le rend plus simple. Par ailleurs, le même problème est perçu simple par les uns et complexe par les autres. Si ce qui précède est juste, le degré de complexité évolue à l’inverse du degré d’apprentissage et d’accoutumance, cette classification ne s’appliquerait donc pas aux problèmes mais à l’évolution de l’apprentissage.
Pourquoi alors un problème est-il plus complexe pour les uns et plus simple pour les autres ?
Il me semble ici qu’il faut distinguer les problèmes qui n’exigent qu’un travail de nature logique de ceux qui exigent un travail analogique. Dans le premier cas, une règle doit être découverte et respectée, il n’y a pas de création réelle. D’une personne à une autre, la ou les mêmes règles seront découvertes. C’est ce qui est arrivé en maths lorsque les divers types de nombres et les diverses opérations arithmétiques ont été découvertes. D’une époque à une autre, d’un peuple à un autre, les mêmes découvertes ont été effectuées en respectant des séquences presque identiques. Ces découvertes se sont déroulées lorsque le problème a été bien perçu. C’est exactement ce qui se produit lorsqu’un enfant avance dans les stades décrits par Piaget. S’il a la maturité neurologique suffisante, bref s’il est entré dans sa période sensible, dès qu’il perçoit clairement le problème, il construit la même solution que tous les autres individus de son espèce.
D’autre part, existent des problèmes où le travail logique suit le travail analogique. Cette fois, il ne s’agit plus de découvrir des règles implicites, mais de saisir d’abord la situation problème dans toute sa complexité, d’imaginer ensuite des solutions possibles, lesquelles peuvent être fort différentes d’un individu à un autre. Ces solutions dépendent largement de la culture d’un individu, de ce qu’il a déjà appris alors que le fonctionnement logique dépend de l’évolution neurologique de l’individu. Par exemple, vers l’âge de 6 ans, l’enfant reconnaît que la quantité de liquide comprise dans un bocal fermé ne varie pas si l’inclinaison du bacal change. Il s’agit d’une évolution en logique. Il n’y a pas d’autres options valables possibles.
Par contre, la pensée analogique est beaucoup plus diversifiée. Ainsi, pour un Chinois, les verbes demeurent à l’infinitif car, lorsqu’une phrase commence par «Demain, nous …» il est déjà clair que l’on parle du futur et, écrire le verbe au futur n’apporte rien de neuf.
L’expérience mentionnée au début de cet échange me semble être strictement du domaine logique en ce qui concerne les proplèmes qualifiés de non-concrets. Par contre, les concrétisations multiples aussi utilisées touchent la culture de l’élève et cette seule variable rend les conclusions douteuses.
J’ai l’habitude, que j’enseigne à des élèves en difficulté ou non, de débuter par un problème qui utilise le moins possible des connaissances qui ne sont pas acquises par tous les élèves. Si le problème est alors réduit à une activité strictement logique, les élèves de 8 ans réussissent avec aisance à résoudre des systèmes d’équations ou à factoriser des trinômes, par exemple. Par contre si un transfert ou une association non implicite devient nécessaire alors là tout est possible. Ce qui m’amène à écrire que je doute que les conclusion de la recherche de Kaminski puissent s’appliquer à la capacité à transférer.
Il me semble aussi que, lorsque nous proposons des problèmes touchant le domaine analogique, nous tentons de rédiger des problèmes «passe-partout» qui ne tiennent pas suffisamment compte de la culture des élèves. Nous créons ainsi des différences importantes dans les chances de réussite des élèves à cause de leur culture et aussi à cause de la … chance. Ou à cause de quelque chose qui fait que soudainement, sans avertissement, jaillit l’idée qui permettra peut-être de résoudre le problème.
Mais j’y pense, lors de la résolution d’un problème de nature logique, il nous faut faire un effort de concentration, il nous faut éviter les distractions. Par contre, l’idée qui permettra peut-être de résoudre un problème de nature analogique jaillit lorsque nous pensons à autre chose ou au réveil ou au milieu de la nuit. C’est toujours la même chose lorsqu’un transfert peu évident est nécessaire. Plus j’y pense, plus il me semble que les conclusions de Kaminski ont peu à voir avec ce qu’il a expérimenté.
Très intéressante discussion. Je voudrais revenir à la tâche donnée en exemple. À y regarder de plus près, il me semble que l’exemple symbolique des tâches, exemple soi-disant abstrait, RESSEMBLE BIEN PLUS au problème posé aux enfants (avec les coccinelles et les vases) que l’exemple soi-disant concret de tasses d’eau mélangées selon une règle fantaisiste (qui va à l’encontre du b.a.-ba arithmétique connu des élèves, et est susceptible de les déstabiliser, voire même d’induire en erreur).
En effet, ce qui diffère entre les tasses est, au premier regard, quantitatif (même si ensuite on peut considérer qu’une tasse contenant x quantité de liquide est une « figure » différente de celle d’une tasse à y quantité de liquide) … alors que la tâche demande à ASSOCIER DES FIGURES INDÉPENDAMMENT DE TOUTE NOTION DE QUANTITÉ.
Autrement dit, en regard de la tâche demandée, l’exemple « symbolique » est bien plus CONCRET et a valeur … D’EXCELLENT EXEMPLE pour le problème posé!
Je dirais donc que, pour le coup, cette étude illustre plutôt le contraire de ce qu’elle prétend prouver.
Moralité: un BON exemple vaut toujours mieux qu’une illu abstraite absconce.
Bonjour, je fais un TFE sur la concrétisation des situations problèmes en mathématiques, et j’aurais voulu avoir plus d’informations sur ce que je viens de lire.
Si vous avez des livres à me faire lire, ou des articles interessants, pouvez – vous me le faire savoir
Bien à Vous
Je suis navré, Aurélie, de ne pas pouvoir vous apporter plus d’information que n’en contient ce billet. Peut-être quelqu’un passant par ici comblera-t-il votre souhait.